Functional Programming Explained: Typeclass(1)

This is the first blog of a long series I would continuously posted over the years, mostly about Functional Programming languages and its features. It is part of my journey to learn Ocaml, Rust, Scala at the same time. The first few of this series would be Types, mostly TypeClasses and DataTypes, this is a long one, and if you are interested to know more, scroll down to the end of the page, I would list all learning materials I come across with through out my journey.

Motivation

People usually know the word Typeclass from Functional worlds, mostly from Haskell I guess as it being the most famous but rarely used functional PL in all industries. But from my short experience with Ocaml, the concept of type class is not very strong but you could feel there must be something there: at least, you heard people talking about Monad all the time😆, you heard about bind function aka >> or (let*) and so on which is heavily used in Option, Result or Futureish types. Of course, the first-class module feature in Ocaml make me feel sort of an usage of “Typeclass” but still not having a concrete understand of it make me feel anxious and I kinda not sure about the fact: Typeclass is useful? Is it?

Thanksfully, while I am reading I came into Cats which have a relative detailed documentation including some practical examples

There are a lot of libraries for different PL implemented Typeclasses, including fp-ts and its successor effect-ts for Javascript, return for Python and finally Cats and Zio for Scala. Unfortunately, most of them does not have great learning resources and documentations which is daunting: The underlying of Typeclass is an advanced math theory called Category Theory, so hard for people like me to have a grasp of.

PS: part of the reason here is that I am not willing to learn Haskell which emphasize pure FP and I am not a big fan of pure. If you are a Haskeller(I don’t know how the community call it) happen to read this, you should not continue reading as you probably have a better understanding of it.

The idea of the rest of this article is heavily borrowed from the book: Scala with Cats, including Figures, thanks to this well-written book, I cannot stop finishing it once I started.

Introduction

There are many Typeclasses, Semigroup, Applicative, Monoid, Monad, Functor…, And they have very complex relationships, thanks for this structure from @Cats.

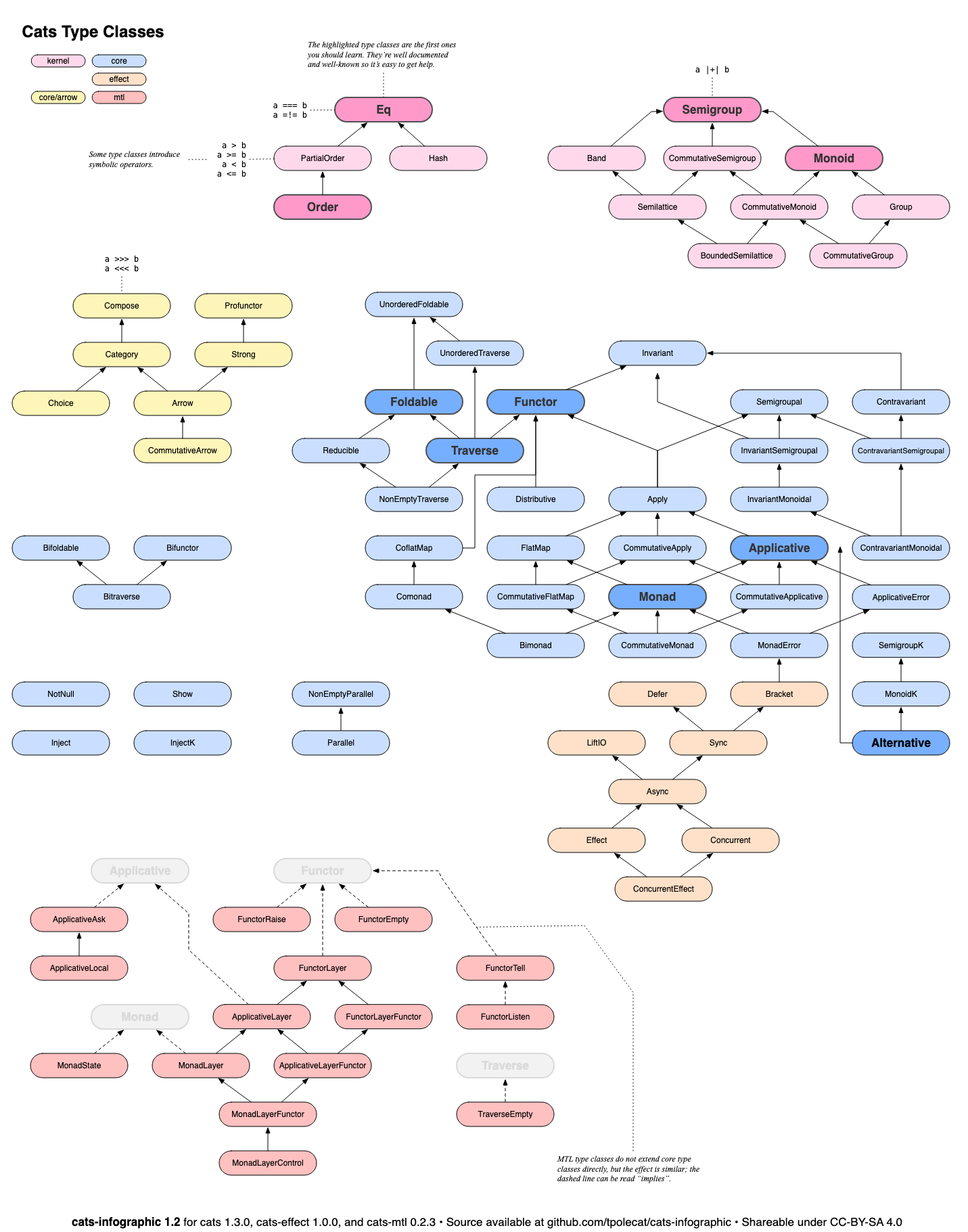
Semigroup

And I would like to talk about Semigroup first(I would show the code using both Ocaml and Scala):

Ocaml

type Semigroup = sig
	type t
	combine: t -> t -> t
end

Scala

trait Semigroup[A] {
	def combine(x: A, y: A): A
}

It seems easy right?

1 + 2 = 3,

“hello” + “world” = “helloworld”

You may say: Huh, Easy MATH.

And indeed, semigroup follows Associativity which we learned back when we are in Primary School:

(1 + 2) + 3 == 1 + (2 + 3)

Hello + (” ” + “world”) == (“Hello” + ” ”) + “world”

But what is the usage of Semigroup? The answer would be answered when we talked about other Typeclass that extends Semigroup and use concrete type to showcase the capability of Typeclasses. Let’s continue.

Monoid

Ocaml

type Monid = sig
	include Semigroup
	empty: t
end

Scala

trait Monoid[A] extends Semigroup[A] {
	def empty: A
}

So let’s implement Monoid first: Ocaml

module IntMonid = struct
	type t = int
	let empty = 0
	let combine x y = x + y
end

module FltMonid = struct
	type t = float
	let empty = 0.
	let combine x y = x .+ y
end

Scala

import cats.Monoid

implicit val intAdditionMonoid: Monoid[Int] = new Monoid[Int] {
  def empty: Int = 0
  def combine(x: Int, y: Int): Int = x + y
}

Then we could do something like: Scala

// For Int
Monoid[Int].combine(1, Monoid[Int].empty)
// For Float
Monoid[Float].combine(1, Monoid[Float].empty)

// You could also do 
val items = List(1,2,3,4);
items.foldleft(Monoid[Int].empty)(Monoid[Int].combine)

In Scala, once we load all instance we want, we could do this for Int, Float, String…all the type that satisfy Monoid typeclass.

💡Small Quiz

1. Implement Monoid for Boolean(hint: there are 4 of them)
2. Implement Monoid for Set(do intersection satisfy Monoid)

not yet finished…